1 Dimensioneringsgrundlaget
Dimensionering – dvs. fastlæggelse af dimensioner på rør, ventiler mv. – kan ifølge vandnormen ske ved beregning.
Der er i dette afsnit givet en kort gennemgang af det teoretiske grundlag, som er nødvendigt for at forstå og kunne gennemføre en dimensionering ved beregning.
Hvis man kun skal arbejde inden for de bygningskategorier, hvor de forenklede beregninger kan anvendes, kan man gå let hen over dette afsnit og blot anvende det, hvor der ønskes en nøjere forståelse.
1.1 Bygningsreglementets krav
Bygningsreglement 2010, kapitel 8.4.2.1, stk. 1 (Erhvervs- og Byggestyrelsen, 2010) kræver, at:
Vandinstallationer skal dimensioneres og udføres, så der opnås en tilfredsstillende vandforsyning ved de enkelte tapsteder under hensyntagen til forsyningsforholdene og til installationens og bygningens anvendelse.
I tilknytning til dette generelle funktionskrav er der i BR10 anført funktionskrav til installationer til koldt vand, varmt vand samt vand til teknisk brug.
For koldt vand anføres bl.a. følgende overordnede krav:
Koldt vand skal ved samtlige tapsteder i fysisk, kemisk og bakteriologisk henseende opfylde de krav, der fremgår af Miljø- og Energiministeriets bekendtgørelse om vandkvalitet og tilsyn med vandforsyningsanlæg (Miljøministeriet, 2006; Miljøministeriet, 2007).
Der skal være en passende koldtvandstemperatur uden besværende ventetid.
For varmt vand anføres bl.a. følgende overordnede krav:
Vandinstallationer skal udformes, så de kan fungere med mindst mulig risiko for bakterievækst.
Anlæg til produktion af varmt brugsvand skal under hensyntagen til varmtvandstapstedernes antal og brug kunne yde en tilstrækkelig vandstrøm med en temperatur der passer til formålet.
En passende varmtvandstemperatur skal være til stede uden besværende ventetid.
Disse overordnede krav gælder for installationen som helhed. De skal være opfyldt ikke alene på udførelsestidspunktet, men også i brugsperioden (en rimelig tid efter ibrugtagning). Se også SBi-anvisning 230, Anvisning om Bygningsreglement 2010, 8.4.2 Vandinstallationer (Hansen, 2010).
For at opnå tilfredsstillende vandforsyning ved tapstederne, skal der tilføres en passende vandstrøm. I bygningsreglementet er det ikke anført, hvad der forstås ved en tilfredsstillende vandforsyning, eller hvordan en vandinstallation skal udformes for at opnå en tilfredsstillende funktion. Der henvises i stedet til vandnormen (Dansk Standard, 2009). Det skal forstås sådan, at en vandinstallation, som er dimensioneret efter retningslinjerne i vandnormen, kan anses for at opfylde bygningsreglementets overordnede krav mht. vandforsyning.
1.2 Sandsynlighed
Der vil sjældent blive tappet vand fra alle tapsteder i en installation samtidig. Tapning fra et givet tapsted på et givet tidspunkt sker altså kun med en vis sandsynlighed. Dimensionering af en vandinstallation er derfor afhængig af, hvor sikker en vandforsyning man vil etablere. Kan man acceptere, at den vandstrøm, der kan tappes, undertiden er mindre end det ønskede? Og i givet fald, må dette forekomme ofte eller kun meget sjældent? Det vil kun undtagelsesvis være nødvendigt at dimensionere en installation, så alle tapsteder kan præstere deres normalydelse samtidig.
Bygningsreglementets overordnede krav om tilfredsstillende vandforsyning ved de enkelte tapsteder fortolkes i vandnormen som en specifik anbefaling af, at en nærmere angivet vandstrøm for de forskellige typer af tapsteder skal kunne ydes med en passende sandsynlighed. For boliginstallationer og lignende angiver vandnormen retningslinjer for, hvad der i almindelighed kan anses for passende, idet dimensioneringsforudsætninger og forsyningstryk er baseret på en vis sandsynlighed. Se afsnit 2, Dimensionering ved beregning, hvori der opstilles nærmere regler.
For byggeri, hvor kravene til vandinstallationen ikke kan sidestilles med kravene til boliger, giver normen retningslinjer i sit Anneks A.
1.3 Energiligningen
Ved beregning af et rørnet holder man regnskab med energien. Det gælder derfor om at få opstillet en ligning, som på en nem måde tillader dette. Selv om det er energien, der regnes med, er det i praktiske beregninger ofte trykket, som indgår i beregningerne.
1.3.1 Tryk og energi
For at forstå sammenhængen mellem tryk og energi kan man tænke sig et stempel indsat i røret i figur 1 øverst. Trykket i væsken er p, og stemplet har et tværsnitsareal på A. Kraften på stemplet bliver da p · A.
Figur 1. Sammenhæng mellem tryk og energi i en strømmende væske.
Væsken strømmer med hastigheden v, og da stemplet følger med væsken, vil det bevæge sig strækningen v i løbet af 1 sekund (da hastigheden er den vej, der tilbagelægges på 1 sekund). Den energi, som væsken indeholder, kan udtrykkes ved det arbejde, den kan udføre. Dette arbejde er lig med kraften på stemplet gange den vej, kraften har virket. Hvis vi ser på det, der sker på 1 sekund, fås:
Ser vi nu på strømningen, vil der på 1 sekund passere et volumen = A · v. Denne størrelse, volumen pr. sekund, kaldes volumenstrøm. Energiindholdet i en volumenenhed af den strømmende væske kan findes som:
Det ses, at talværdien for energiindholdet pr. volumenenhed er lig med talværdien for trykket. I mange tilfælde er det ved beregning mest praktisk at anvende trykket, fordi det er en størrelse, som ret let kan måles, men det er alligevel energien, man holder regnskab med.
1.3.2 Tryk og højde
En anden størrelse, som ofte anvendes til at karakterisere energiind-hold, er 'højde'. Man kan let se, hvordan tryk og højde kan anvendes sideordnet ved hjælp af figur 2, idet tryk er defineret som kraft pr. fladeenhed.
Figur 2. Sammenhæng mellem tryk og højde i en væske.
Den kraft, hvormed den skraverede væskemasse trykker på arealet A i karrets bund, er tyngdekraften på det skraverede volumen:
hvor
Trykket \rho kan altså her beregnes som højde · densitet · tyngdeacceleration. Da g og ρ er konstanter (forudsat samme væske), kan højden altså bruges som udtryk for trykket og dermed for energien. Hvis det skal præciseres, hvilken væske der menes, kan det nævnes efter højdeangivelsen, fx mH2O (meter vandsøjle, skrives ofte mVS), eller mmHg (millimeter kviksølv).
Disse størrelser kan umiddelbart omsættes til andre trykenheder efter tabel 3 og 4 i SBi-anvisning 234, Vandinstallationer – funktion og tilrettelæggelse.
1.3.3 Energiindhold i en strømmende væske
En væskedel, der befinder sig i en strømmende væske, har på et givet tidspunkt et energiindhold, der er afhængig af væskedelens højde z over et givet udgangsniveau, væsketrykket p og væskedelens strømningshastighed v. Det totale energiindhold pr. volumenenhed af væsken kan da skrives:
hvor
Det ses, at energiindholdet er karakteriseret ved tryk. Ligningens højre side indeholder 3 led, som hver karakteriserer en bestemt type mekanisk energi.
Potentiel energi, \rho\cdot g\cdot z , er den energi, en væskedel har, fordi den har en vis højde over et referenceniveau. Hvis fx vandet i en beholder står i en vis højde over en åbning i bunden, kan vandet selv strømme ud, fordi det har denne potentielle energi (eller beliggenhedsenergi).
Trykenergi, p, står for den energi, som væskestrømmen har, fordi den kan bevæge et stempel og dermed udføre et arbejde. Trykket p kaldes det statiske tryk, også selv om væsken er i bevægelse. Betegnelsen statisk er nødvendig, fordi væsken også har et dynamisk tryk, som direkte afhænger af strømningshastigheden.
Kinetisk energi, 1/2\cdot\rho\cdot v^2 , betegner den energi, som væskedelen har, fordi den har en hastighed og derfor kan udføre et arbejde. Denne energi kaldes kinetisk energi (eller hastighedsenergi). Med trykbetegnelse kaldes $$ 1/2\cdot\rho\cdot v2 $$ $$ 1/2\cdot\rho\cdot v2 $$ for det dynamisk tryk. Det dynamiske tryk opfattes som den trykstigning, man ville få i væsken, hvis man bremsede væskestrømmen.
Den totale energi, ptot, betegner væskedelens totale energiindhold eller det totale tryk. I praksis bruger man betegnelsen det totale tryk for summen af statisk og dynamisk tryk. I figur 3 er vist, hvordan statisk, dynamisk og totalt tryk kan måles. Det er praktisk at operere med tryk, fordi de kan måles.
Figur 3. Statisk, dynamisk og totalt tryk i en strømmende væske. For væsker i hvile er det dynamiske tryk nul, og det totale tryk er derfor lig med det statiske tryk.
1.3.4 Energiindhold udtrykt ved højder
Hvis man dividerer alle leddene på højre side i ligning 5 med \rho\cdot g , så bliver første led kun z – altså en højde – og tilsvarende får de andre led også dimension af højde:
Her er trykket, pH, angivet som højden af en vis væskesøjle. De to sidste led benævnes trykhøjde og hastighedshøjde. Denne version af ligningen, som ofte benævnes trykhøjdeligningen, anvendes, når der regnes i meter vandsøjle, hvilket der traditionelt er gjort ved beregning af vandinstallationer.
1.3.5 Energitab ved strømning
Når vand strømmer i et rør tabes der energi på grund af gnidning mellem væske og rørvæg og mellem væskedelene indbyrdes. Den tabte energi omsættes til varme og må derfor i vandinstallationen anses for tabt. Vandets totale energi pr. volumenenhed aftager således i strømningens retning, og betragtes to punkter, 1 og 2, i en vandinstallation, kan man udtrykke det således:
Ligningen udtrykker blot, at energitabet fra pkt. 1 til pkt. 2 er lig med forskellen i energiindhold de to steder. Indsættes udtrykket for ptot, ligning 5, fås:
som kan omskrives til:
Ligning 9 betegnes energiligningen for strømning.
For vand kan udtrykket skrives:
hvor
z er højden [m]
p er det statiske tryk [kPa]
v er strømningshastigheden [m/s].
Hastighedsfordeling
Udtrykket for kinetisk energi er opstillet under forudsætning af, at hastigheden er konstant over hele strømningstværsnittet. Det er den ikke. Normalt korrigeres for dette ved hjælp af en hastighedsfordelingskoefficient α, så den kinetiske energi angives som:
α afhænger af strømningsformen og kan med tilnærmelse sættes til 1,1 for en turbulent strømning. Ved almindelige dimensioneringsberegninger er det imidlertid tilladeligt at se bort fra det dynamiske tryk, dels fordi det falder bort ved tryktabsberegninger for lige rør, dels fordi det er lille sammenlignet med det statiske tryk. Energiligningen, ligning 9, forenkles derved til:
Angives trykket som højder – som tidligere var mest almindeligt – får energiligningen formen:
hvor
1.3.6 Energilinjen
Hvis man vil danne sig et overblik over variationerne i vandets totale tryk eller energiindhold, kan det ske ved optegning af en kurve over forløbet langs strømningsvejen. Kurven, som betegnes energilinjen, bestemmes ved, at man først fastlægger det totale tryk ved rørstrækningens begyndelse og derefter fører regnskab med tabene langs strækningen. Disse beregninger beskrives i afsnit 1.4, Energitab. Et eksempel på forløbet af en energilinje er vist i figur 4.
Figur 4. Optegning af energilinje langs en rørstrækning. I hvert punkt angiver energilinjen summen af potentiel energi, trykenergi og kinetisk energi.
Når energilinjen kendes, kan de enkelte bidrag til energiindholdet beregnes. Den potentielle energi kan findes direkte ud fra kendskab til rørledningens geometri, og den kinetiske energi kan beregnes ud fra rørdiameter og vandstrøm.
Sluttelig kan det statiske tryk, p, findes som:
1.4 Energitab
For at kunne gennemføre en dimensionering må de energitab eller tryktab, som sker langs en rørstrækning, kunne beregnes.
Tryktabene i rørsystemet opdeles i to forskellige grupper, nemlig:
- Lige rør (med konstant tværsnit)
- Enkeltmodstande.
Enkeltmodstande udgøres af bøjninger, armaturer og lignende – kort sagt alt det, som ikke er lige rør.
1.4.1 Tryktab i lige rør
Tryktabet i lige rør afhænger af mange forhold, fx rørlængde, strømningsform, vandtemperatur, rørdiameter og rørets ruhed. Tryktabet kan angives som:
hvor
l er ledningslængden [m]
d er ledningens indvendige diameter [m]
v er strømningens middelhastighed [m/s].
Reynolds' tal
Friktionskoefficienten er en funktion af et andet dimensionsløst tal kaldet Reynolds' tal, Re:
hvor
v er strømningens middelhastighed [m/s]
d er ledningens indvendige diameter [m]
υ er den kinematiske viskositet [m2/s].
Den kinematiske viskositet er et udtryk for, hvor tyktflydende vandet er, og den er afhængig af temperaturen, se tabel 1.
Tabel 1. Vands kinematiske viskositet ved forskellige temperaturer.
Vandtemperatur [°C] | 0 | 10 | 20 | 30 | 40 | 60 | 80 | 100 |
|---|---|---|---|---|---|---|---|---|
Kinematisk viskositet [m2/s10-6] | 1,78 | 1,30 | 1,00 | 0,81 | 0,66 | 0,48 | 0,37 | 0,29 |
Reynolds’ tal Re er en meget vigtig strømningsparameter. Den registrerer således omslaget mellem laminar og turbulent strømning, hvilket teoretisk sker ved Re = 2300. Der må i praksis regnes med et vist interval, hvor strømningen er instabil, og hvor tryktabet ikke kan forudberegnes. I almindelighed regner man med, at dette område er afgrænset til 2000 < Re < 3000.
Laminar strømning
Såfremt Re < ca. 2000, kan man regne med, at strømningen er laminar, dvs. der er tale om en roligt flydende strøm med parallelle strømlinjer. Ved laminare strømninger er friktionskoefficienten uafhængig af rørets ruhed, og den kan direkte beregnes til:
Turbulent strømning
Såfremt Re > ca. 3000, vil strømningen være turbulent, dvs. strømningen er urolig og med strømhvirvler (strømlinjerne er ikke parallelle). For en turbulent strømning kan friktionskoefficienten ikke beregnes teoretisk, men der findes mange erfaringsformler.
Colebrook-White's formel
Den formel, som betragtes som den bedst egnede, er Colebrook-White's formel. Formlen er baseret på såvel målinger som teoretiske overvejelser. Den dækker ikke eksakt alle typer af ruhed, men den giver en god tilnærmelse for de rørtyper, der anvendes i praksis.
Friktionskoefficienten beregnes med Colebrook-White's formel, som lyder:
hvor
λ er friktionskoefficienten (dimensionløs)
Re er Reynolds' tal (dimensionløs)
k er rørets ruhed [m]
d er indvendig diameter [m].
Rørets ruhed skal karakterisere den indvendige røroverflade. Den angives som længdemål [m]. Ruheden afhænger ikke alene af højden af ujævnhederne, også ujævnhedernes form og antal har betydning for strømningsmodstanden. Ruheden afhænger således både af rørmateriale og fremstillingsmetode og kan bestemmes ved strømningsmåling. Værdier for forskellige rørtyper er angivet i tabel 2.
Tabel 2. Ruheden k for forskellige rørtyper. Disse ruheder er anvendt ved udarbejdelse af nomogrammerne i figur 7-11. For rør af rustfrit stål kan man med god tilnærmelse anvende samme ruheder og nomogrammer som for kobberrør.
Materiale | Indvendig overflade | Ruhed, k [m] |
|---|---|---|
Kobberrør, rustfri stålrør | Uden afsætninger | 0,0000015 |
Med afsætninger | 0,00015 | |
Plastrør | 0,00001 | |
Stålrør | Varmforzinkede med afsætninger | 0,001 |
Varmforzinkede uden afsætninger | 0,00015 | |
Støbejernsrør1) | Nye, asfalterede | 0,00015 |
1) Asfalterede støbejernsrør anvendes kun til særlige formål, hvor andre rørtyper er uegnede.
Formlen er ikke let at anvende, da friktionskoefficienten ikke kan beregnes direkte, men må beregnes ved iteration.
I stedet kan følgende formler anvendes til direkte beregning af tryktabet i lige rør:
hvor
Symboler og enheder er som angivet i formel 18.
Ved anvendelse af formel 19 er afvigelserne fra Colebrook-White's formel mindre end -1/+3 %.
Colebrook-White's formel anvendes mest til fremstilling af diagrammer hvor friktionskoefficienten kan aflæses i de aktuelle tilfælde. Et eksempel på et sådant diagram er Moody’s diagram, se figur 5.
Figur5. Friktionskoefficienten λ som funktion af Reynolds' tal Re og den relative ruhed. Diagrammet, der betegnes Moody's diagram, anvendes som anført i teksten herunder.
Anvendelsen af Moody's diagram sker på følgende måde: Først bestemmes Reynolds tal:
hvor
v er strømningens middelhastighed [m/s]
d er ledningens indvendige diameter [m]
υ er den kinematiske viskositet [m2/s], se tabel 1.
Derefter bestemmes den relative ruhed k/d, hvor k er ruheden, se tabel 2, og d er ledningens indvendige diameter (m). Med Reynolds’ tal og den relative ruhed som indgangsværdier findes friktionsværdien λ af diagrammet. Tryktabet pr. m rør er da givet ved:
hvor
R er tryktabet pr. meter rørstrækning [Pa/m]
λ er friktionskoefficienten
d er ledningens indvendige diameter [m].
På grundlag af Moody's diagram kan der udarbejdes tabeller eller diagrammer over tryktab i forskellige rørtyper.
1.4.2 SBi-(tryktabs)nomogrammer
SBi har på grundlag af Colebrook-White’s formel udarbejdet en serie (tryktabs)nomogrammer gældende for de hyppigst anvendte rørtyper, se figur 7-11. Nomogrammerne anvendes som vist i figur 6.
Figur 6. Anvendelse af tryktabsnomogrammer. Man kan gå ud fra to vilkårlige akser. Hvis fx vandstrømmen og tryktabet kendes, kan disse to akser anvendes som udgangspunkt. Vandstrøm og tryktab afmærkes på de respektive akser. Gennem de to punkter trækkes en ret linje til skæring med de øvrige akser, og rørdiameter og hastighed samt dynamisk tryk kan findes ved skæringspunkterne med de to øvrige akser.
Aksen for dynamisk tryk anvendes i forbindelse med enkeltmodstande, se afsnit 1.5, Tryktab i enkeltmodstande. Bemærk, at nomogrammernes enhed for tryktab er Pa – og ikke kPa, som anvendes i vandnormen og i denne anvisning.
Aksen for dynamisk tryk anvendes i forbindelse med enkeltmodstande, se afsnit 1.5, Tryktab i enkeltmodstande. Bemærk, at nomogrammernes enhed for tryktab er Pa – og ikke kPa, som anvendes i vandnormen og i denne anvisning.
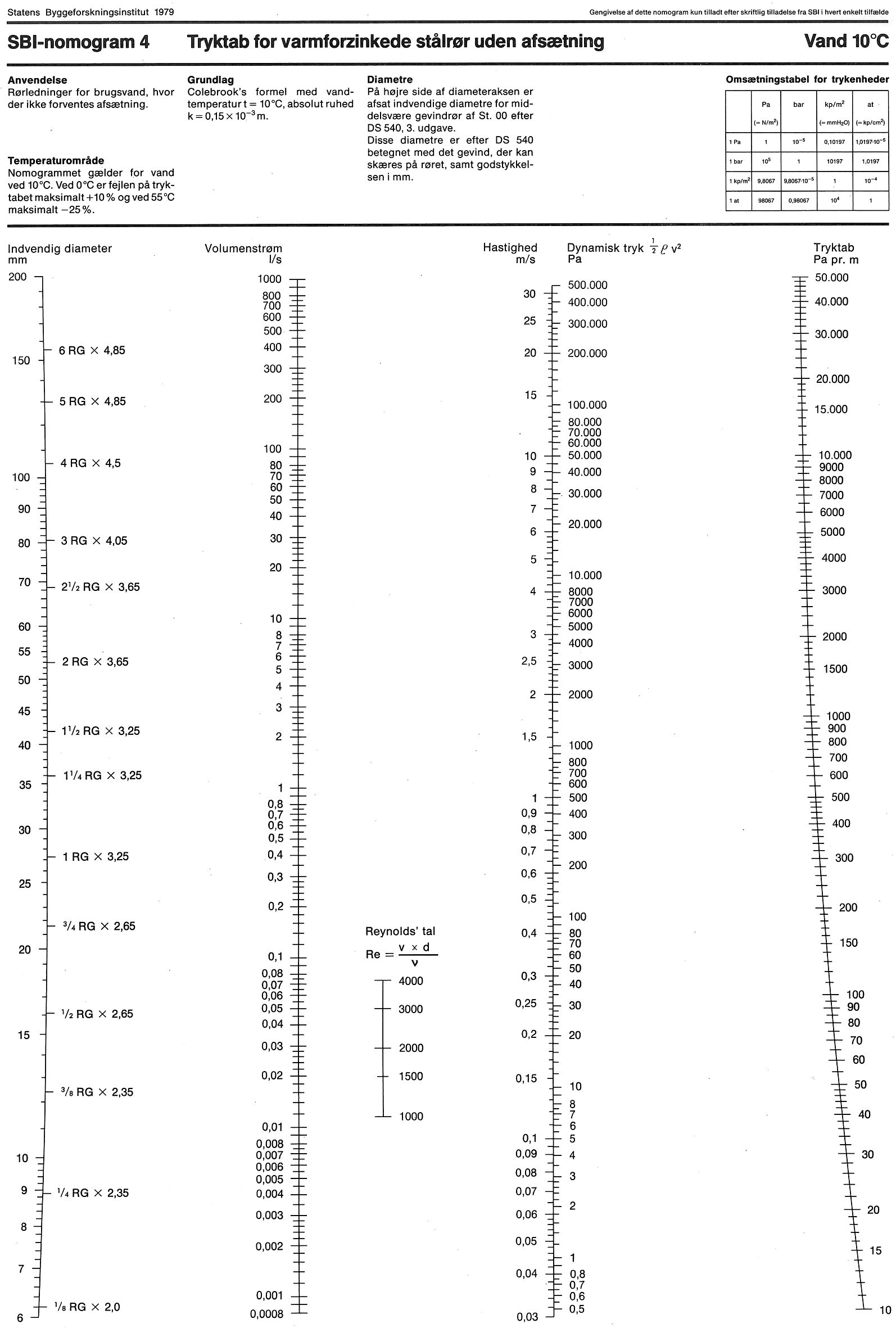 |
Figur 7. Tryktab for varmforzinkede stålrør uden afsætning.
 |
Figur 8. Tryktab for varmforzinkede stålrør med afsætning.
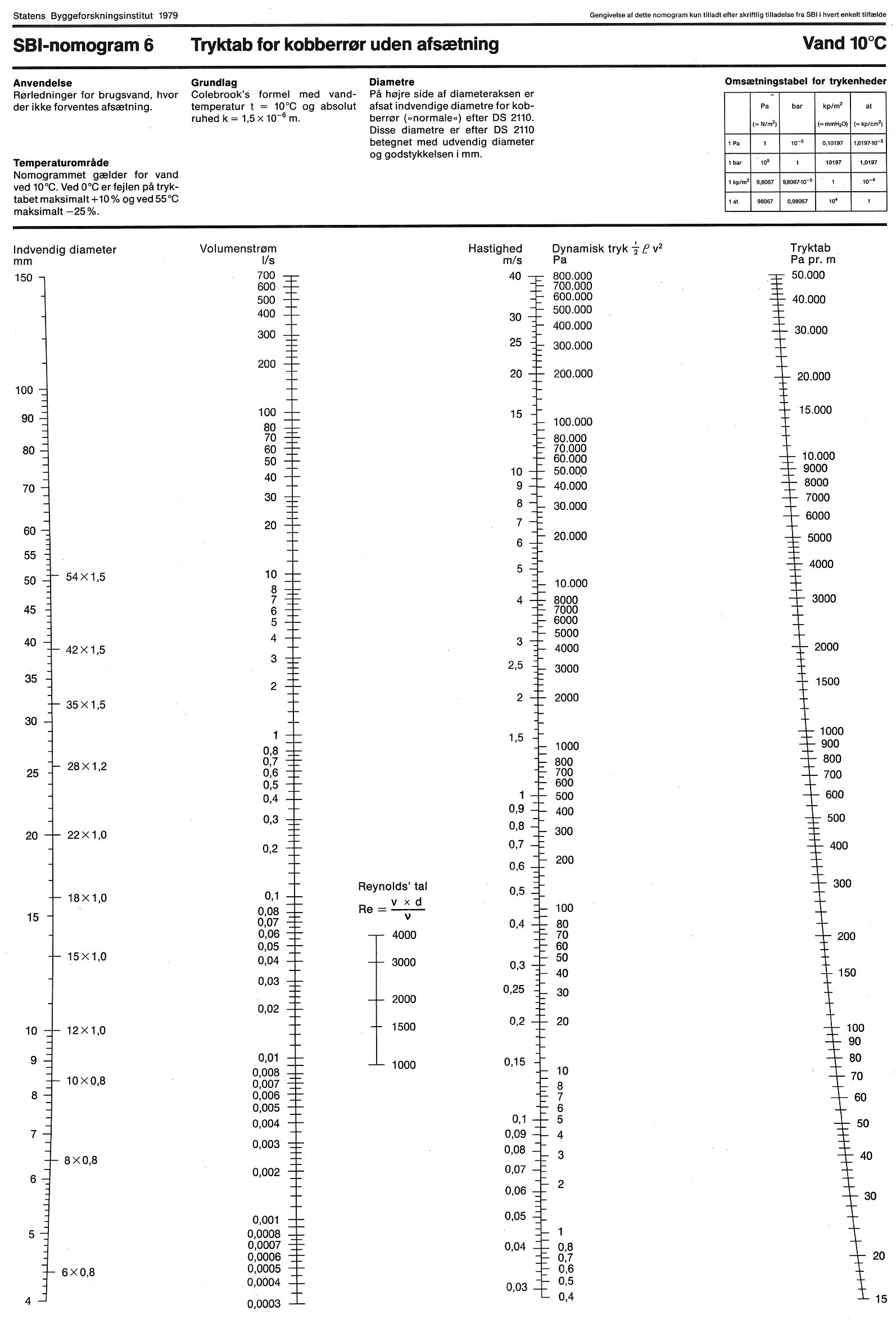 |
Figur 9. Tryktab for kobberrør og rustfri stålrør uden afsætning.
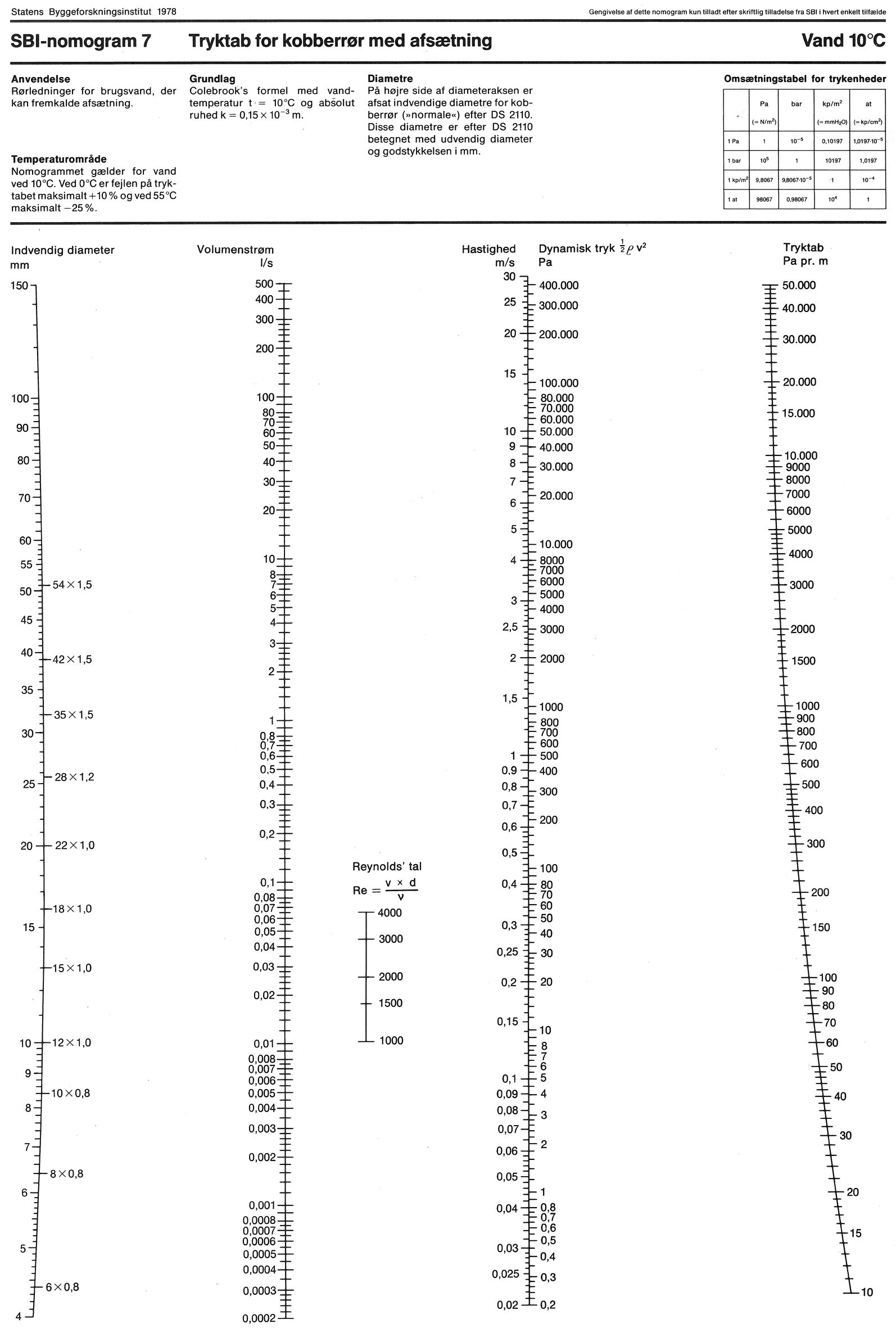 |
Figur 10. Tryktab for kobberrør og rustfri stålrør med afsætning.
 |
Figur 11. Tryktab for plastrør. Nomogrammet er beregnet for pe-ledninger til koldt vand. For pex og alu-pex til varmt vand henvises til diagrammer fra rørleverandørerne. Nomogrammerne er oprindelig udarbejdet til brug sammen med standarderne, nævnt øverst i figuren. Selvom disse standarder er erstattet af nyere, er nomogrammerne stadig anvendelige.
1.5 Tryktab i enkeltmodstande
Hver gang strømmende vand ændrer hastighed, taber vandet energi, dvs. der opstår et tryktab. Det gælder, både når hastigheden ændres i retning, og når den ændres i størrelse. Hastighedsændringer sker mange steder i en installation, fx i bøjninger, i armaturer, ved dimensionsændringer og ved ind- og udløb i beholdere. Under et kaldes disse fysiske årsager til hastighedsændringer for enkeltmodstande.
Størrelsen af tabet i en enkeltmodstand afhænger af dens form. En jævnt forløbende strømning gennem enkeltmodstanden giver mindre tryktab end en strømning, hvor der sker mange og bratte hastighedsændringer. En strømningsændring, hvor hastigheden vokser, giver mindre tab end en, hvor hastigheden aftager.
1.5.1 Beregning af tryktab i enkeltmodstand
Tryktabet i en enkeltmodstand kan udtrykkes ved modstandstallet, ζ, og kan beregnes af formlen:
hvor
Modstandstallet er et karakteristisk tal for den pågældende enkeltmodstand. I tabel 3 er angivet modstandstal for nogle hyppigt forekommende enkeltmodstande.
Tabel 3. Modstandstal for enkeltmodstande. For VA-godkendte ventiler mv. er der i godkendelsen angivet ζ-værdier for
forskellige dimensioner. VA-godkendelserne viser også kurver med sammenhængen mellem tryktab og vandstrøm.
Modstandstal og tryktabskurver kan også oplyses af fabrikanterne.
forskellige dimensioner. VA-godkendelserne viser også kurver med sammenhængen mellem tryktab og vandstrøm.
Modstandstal og tryktabskurver kan også oplyses af fabrikanterne.